Radiative Forcing from a change in atmospheric CO₂ concentration

By Dave Burton, Oct. 11, 2020.  (Adapted, in part, from a blog comment.)
Last updated: Jan. 1, 2024.

• Synopsis:  https://sealevel.info/Radiative_Forcing_synopsis.html
• Similar calculations for CH₄: https://sealevel.info/methane.html

Contents:

1. Calculated estimates of CO₂'s radiative forcing
2. Measurements of CO₂'s radiative forcing
    2.1 Feldman, 2015
    2.2 Rentsch, 2020
    2.3 Kramer, 2021
3. Warming effect of radiative forcing

1. Calculated estimates of CO₂ forcing

The formula for estimating radiative forcing (RF) from a change in atmospheric CO₂ concentration is usually given as:
    ΔF = 𝞪·ln(C/C₀) W/m²
    ΔF = ERF·log₂(C/C₀) W/m²
where:
    C/C₀ is the ratio of new to old CO₂ concentrations, and
    ERF = 𝞪·ln(2) = “Effective Radiative Forcing” per doubling of CO₂ level
and the most common estimate is:
    𝞪 = 5.35 ±0.58

For a doubling of CO₂ concentration that yields:
    ERF = 𝞪·ln(2) = 3.7 ±0.4 W/m² per doubling of CO₂ concentration

That's the figure mostly used by the IPCC (TAR & later). It is from Myhre 1998 (pdf), though Myhre preposterously claimed an uncertainty of only 1%. The more realistic ±0.4 W/m² confidence interval (per doubling of CO₂) is from 'Step 4' of Gavin Schmidt's 2007 RealClimate post. (That would be about ±0.58 for 𝞪.) AR5 gives a similar uncertainty of “10%”.

That represented about a 15% reduction from an earlier (FAR Table 2.2 p.52, and SAR §6.3.2 p.320) IPCC estimate of:
    𝞪 = 6.3  (which is ERF=4.4 W/m² per doubling)

Prof. Will Happer (2013) reported calculating [2], based on corrected modeling of CO₂ lineshapes, that Myhre's widely used “5.35” coefficient is about 40% too high. (See also Happer 2015.) That makes:
    𝞪 ≈ 3.8 ±0.5  (which is 2.6 ±0.5 W/m² per doubling)

Etminan, Myhre, Highwood & Shine (2016) reported a more complex formula which is similar to Myhre (1998), but with 𝞪 very slightly smaller for small CO₂ level changes, and 𝞪 slightly larger for large future CO₂ level changes; see details here. They claimed a 10% uncertainty.

van Wijngaarden & Happer (2021) (preprint) (and 2020 & 2022) report calculating CO₂'s ERF at the mesopause (similar to TOA) to be 2.97 W/m² per doubling (see their Table 2 [or 2020 version, or 2022 update], rightmost column). That makes:
    𝞪 = 4.28

The IPCC's AR5 reported that the radiative forcing estimates for a doubling of CO₂ assumed in 23 CMIP5 GCMs vary from 2.6 to 4.3 W/m² per doubling, so that:
    𝞪 ≈ 3.7 to 6.2

Prof. Joshua Halpern reports:
    𝞪 = 4.35  (I don't know his source; I asked, but he didn't answer):

2. Measurements of CO₂'s radiative forcing

Feldman et al 2015 measured downwelling longwave IR “back radiation” from CO₂, at ground level, under clear sky conditions, for jsut over a decade, to determine the effect of increasing atmospheric CO₂ concentration. They reported that a 22 ppmv increase (+5.946%, starting from 370 ppmv in 2000) resulted in a 0.2 ±0.06 W/m² increase in downwelling LW IR from CO₂. A 5.946% concentration increase yields a 8.333% forcing increase, which happens to be almost exactly 1/12 of a doubling, which makes their measured result 12 × (0.2 ±0.06 W/m²) = +2.40 ±0.72 W/m² per doubling of CO₂.

However, radiative forcing is customarily defined at TOA, not at the surface. That is, it's specified in terms of an equivalent change in solar radiation. The effect of GHGs on radiation balance at the surface is similar, but not identical, to their effect at TOA.

The only way that energy leaves the Earth at TOA is by radiation, but at the Earth's surface the energy fluxes are much more complicated, including important mechanisms like convection and evaporative cooling. Warming the Earth causes its rate of cooling to increase by all of those mechanisms, making them negative feedbacks. Those negative feedbacks limit the temperature increase which results from an increase in any forcing.

GHGs in the atmosphere have their effect on temperature by absorbing outbound longwave IR radiation from below, which otherwise would have escaped to space. Absorbing that radiation warms the atmosphere. That, in turn, increases radiation from GHGs in the atmosphere, about half of which goes back down toward the surface, as “downwelling” or “back radiation,” which warms the surface. Hence, the surface and the lower troposphere warm or cool together.

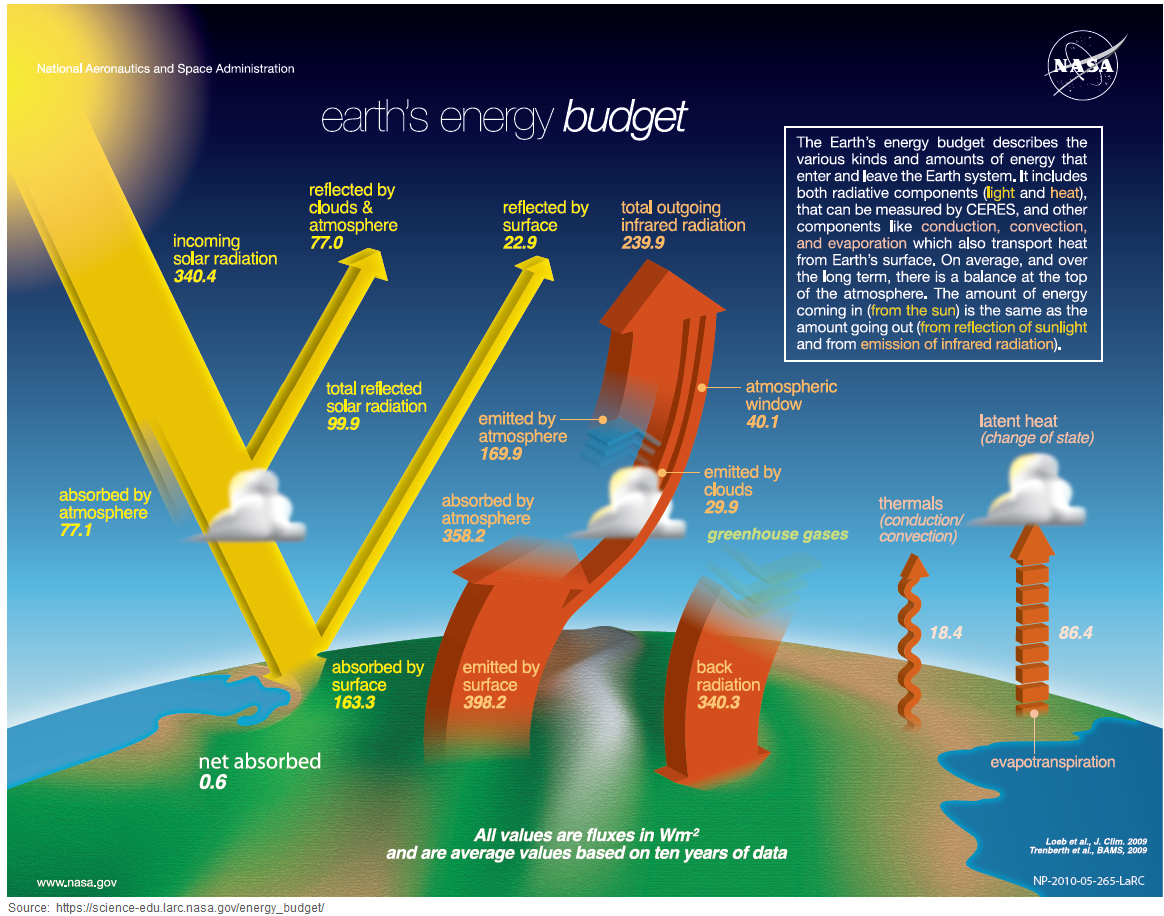
Here's NASA's 2014 (latest?) version of the famous Trenberth energy flow diagram (click to enlarge it):

The diagram was discussed on WUWT, here:
https://wattsupwiththat.wordpress.com/2014/01/17/nasa-revises-earths-radiation-budget-diminishing-some-of-trenberths-claims-in-the-process/

The diagram shows:

1. Incoming solar radiation at TOA = 340.4 W/m². That's one-fourth of 1361.6 W/m², which is their estimate for the average value of the “Solar Constant.” (The so-called “Solar Constant” actually varies somewhat, and other estimates for its average vary from 1360 to 1370 W/m².) ↑

It's one-fourth because the 1361.6 W/m² figure is solar radiation intensity at TOA, where the Earth directly faces the Sun, and the 340.4 figure is averaged over the entire globe, including the back side. (The surface area of a sphere is exactly four times the area of a circle of the same radius.)

2. NASA's estimate of outgoing radiation at TOA is 239.9 W/m² IR + 77.0 + 22.9 = 339.8 W/m², which is 0.6 W/m² less than the incoming solar radiation. That figure is called the “radiative imbalance.” ↑

The “radiative imbalance” (a/k/a “Earth's energy imbalance”) represents warming “in the pipe,” but not yet realized.

It is poorly constrained, and not directly measurable. I’ve also seen estimates of 0.7 or 0.8 W/m². Calculation from realistic estimates of other common climate parameters yields a radiative imbalance estimate of about 0.3 W/m².

A radiative imbalance of 0.6 W/m² would mean roughly 0.6 × 0.3±0.1°C ≈ 0.2 °C, or 0.6 / 2.2±0.2 ≈ 0.3 °C of unrealized warming, depending on sensitivity estimates. ↑

3. Downwelling “back radiation” at the surface, from GHGs in the atmosphere, is estimated as averaging 340.3 W/m². That's about the same as the solar irradiance at TOA, but ≈29% greater than the average amount of solar radiation which makes it to the surface. ↑

4. About 22.6% (77 W/m²) of the incoming solar radiation is reflected back into space, without either reaching the surface or being absorbed. ↑

Thus, an increase of 1 W/m² in LW IR at the surface from GHGs in the atmosphere has an effect on surface temperatures which is similar to a (1 / 0.774) = 1.29 W/m² increase in average solar irradiance at TOA (like a 5.17 W/m² increase in the Solar Constant).

That 1.29:1 ratio is approximate, because the effect of sunlight at the surface is not identical to the effect of downwelling LW IR from atmospheric CO₂. On one hand, there's some overlap between the spectrums of CO₂ and water vapor, which reduces the warming effect from CO₂, especially in the humid tropics. On the other hand, an estimated 22.9 W/m² (6.7%) of sunlight is reflected from the surface back into space, which does not happen for LW IR. If that 6.7% were included in the calculation above, it would make an an increase of 1 W/m² in downwelling LW IR at the surface similar in effect to a (1 / 0.706) = 1.42 W/m² (rather than 1.29 W/m²) increase in average solar irradiance at TOA, like a 5.66 W/m² increase in the Solar Constant.

Adjusting the Feldman values for having measured at the surface, rather than TOA, yields about 1.29 × (2.40 ±0.72) per doubling at TOA, and dividing by ln(2), yields the coefficient:
    𝞪 = 4.47 ±1.34  (which is 3.10 ±0.93 W/m² per doubling)

That figure is very close to van Wijngaarden & Happer's “4.28” and Halpern's “4.35”, and closer to Happer's “3.8” than to Myhre's “5.35,” but the uncertainty interval is wide enough to encompass all four estimates. It does preclude the SAR's “6.3” figure.

Rentsch 2020 (unpublished draft), analyzed orbital Atmospheric Infrared Sounder (AIRS) spectroscopy, and found that CO₂-induced radiative forcing at TOA from a 37 ppmv CO₂ concentration increase (13.65% of a doubling), under nighttime, cloud-clear conditions, caused +0.358 ±0.067 W/m² radiative forcing increase. Dividing by 0.1365 × ln(2), yields the coefficient:
    𝞪 = 3.79 ±0.71  (which is 2.62 ±0.49 W/m² per doubling)

That's about 70% of the Myhre 1998 / IPCC prediction, and very close to Happer's result.

Kramer, RJ et al. 2021. Observational evidence of increasing global radiative forcing. Geophysical Research Letters, 48, e2020GL091585. doi:10.1029/2020GL091585 (preprint) (article).
They report a TOA radiative forcing change of 0.53±0.11 W/m² from 2003 to 2018, of which they attribute 0.43±0.10 W/m² to rising GHG concentrations, and 0.10±0.05 W/m² to air pollution abatement (though they note that the latter “may have a greater direct impact than inferred by [their analysis], which does not include aerosol cloud albedo effects…“).
Per Mauna Loa measurements, average atmospheric CO2 concentration rose from 375.98 ppmv in 2003 to 408.72 ppmv in 2018. log2(408.72/375.98) = 0.12046, so that increase was about 12% of a doubling.
CH4 concentration rose from 1.7774 ppmv in 2003 to 1.8573 in 2018. According to MODTRAN, the CH4 increase should have accounted for about 298.488 - 298.426 = 0.062 W/m². If CO2 and consequent feedbacks accounted for the rest, that leaves 0.43±0.10 - 0.06 = 0.37±0.10 W/m² (he apparently estimates 0.364 W/m² from CO2), from a 12% CO2 forcing increase (due to an 8.7% CO2 concentration increase).
So ERF at TOA from a doubling of CO2 + feedbacks should be (0.364±0.11) / 0.12046 = 3.02 ±0.83 W/m². Kramer's central estimate is noticeably less than the Myhre 1998 and IPCC (TAR & later) estimates for radiative forcing from CO2 alone, without feedbacks (3.7±0.4 W/m² per doubling), but the confidence intervals overlap.
Kramer's result isn't directly comparable to their figures, because his result includes the effects of immmediate feedbacks, but if they had no net effect then his result would imply 𝞪 is 4.43 ±1.20 (compared to Myhre's 5.35 ±0.58). Like Feldman's similar figure, that is very close to van Wijngaarden & Happer's 4.28, and closer to Happer's 3.8 than to Myhre's 5.35, but the uncertainty interval is wide enough to encompass all three estimates.

3. Warming effect of radiative forcing

To get a feel for what such RF values imply for temperatures, consider that it is calculated that a uniform global temperature increase of 1°C would increase radiant heat loss from the surface of the Earth by about 1.4% (variously estimated to be 3.1 to 3.7 W/m², or 3.1 to 3.3 W/m² in the CMIP5 models — it's complicated). That suggests that a 3 W/m² forcing increase should result in a bit less than 1°C of average eventual warming, and that 0.53 W/m² over 1.5 decades (per Kramer et al) should yield a warming trend of about +0.11°C/decade, which is about right.

However, Koll & Cronin (2018) report that, in practice, with feedbacks, the relation under clear sky conditions is (surprisingly!) approximately linear, and only about 2.2 W/m² per °C (±10%). That means a 3 W/m² forcing increase (from a doubling of atmospheric CO₂ concentration) should result in about (3 / 2.2) = just under 1.4°C of average eventual surface warming. (That is an estimate of ECS climate sensitivity.) ↑

That relation also gives us a way to estimate warming that is "still in the pipeline," due to current TOA radiative imbalance. That's more or less the temperature difference resulting from the difference between ECS and TCR (except, from all forcings, not just CO2). TOA radiative imbalance is typically estimated as 0.6 to 0.8 W/m², though it's actually probably closer to 0.3 W/m². A radiative imbalance of 0.7 W/m² represents only about 0.3°C of eventual warming "in the pipe" (which is nearly negligible, for practical purposes).
 

• For a deeper dive into “climate sensitivity” (the quantified warming effect of CO₂) see:
https://sealevel.info/sensitivity.html

• For graphs of atmospheric CO₂ concentration see: https://sealevel.info/co2.html

• For CO₂ emissions data see: https://sealevel.info/carbon/